Vector Dot Product Intuition

Page Purpose

This page is designed to give intuition to the vector dot product (written for vectors u and v as u⋅v, or effectively via matrix multiplication as uᵀv or as an inner product ⟨u, v⟩). The phrase

“The dot product of u and v is just the degree by which each are in the same direction, scaled by their actual lengths.”

is the important takeaway here; the rest of the information on this page exists to clarify exactly why that is/ give examples and visual intuition.

Overview

The dot product of u and v is given by

$\mathbf{u} \cdot \mathbf{v} = \textup{cos}(\theta_{\mathbf{u}, \mathbf{v}}) \left \| \mathbf{u} \right \| \left \| \mathbf{v} \right \|$

In other words, the dot product of u and v is just the degree by which each are in the same direction, scaled by their actual lengths.

This, intuitively, ranges from 0 (when they are perpendicular) to |u||v| (when they are codirectional) to –|u||v| (when they are antidirectional).

Via scalar projections

Put another way,
$\mathbf{u} \cdot \mathbf{v} = u_\mathbf{v} \left \| \mathbf{v} \right \|$ , where $u_\mathbf{v}$ is the scalar projection of u onto v
$\mathbf{u} \cdot \mathbf{v} = v_\mathbf{u} \left \| \mathbf{u} \right \|$ , where $v_\mathbf{u}$ is the scalar projection of v onto u

So u · v is just the amount of u in the direction of v, scaled by the magnitude of v — and vice-versa.

As a concrete example of this, consider that the dot product of a vector A with a unit vector û just gives you the amount of A in the direction of û, as û provides a x1 scaling after scalar projection.
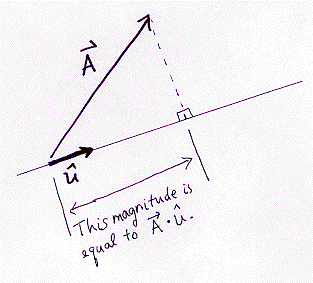
$The dot product of a vector A with a unit vector û is just A projected onto û's line - the amount of A in the direction of û$

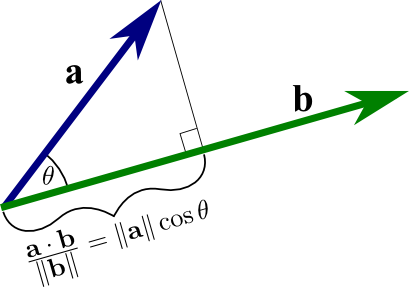
The below image provides some summarizing visual intuition behind the scalar projection’s relationship to the dot product. a · b/||b|| and |a|cos(θ) are both valid ways of writing $a_\mathbf{b}$ (the scalar projection of a onto b), and multiplying it by b so yields the dot product.
$Dot product intuition$

Via component-wise multiplication dot product definition

The image below provides a derivation of the cosine dot product definition via the component-wise dot product definition.
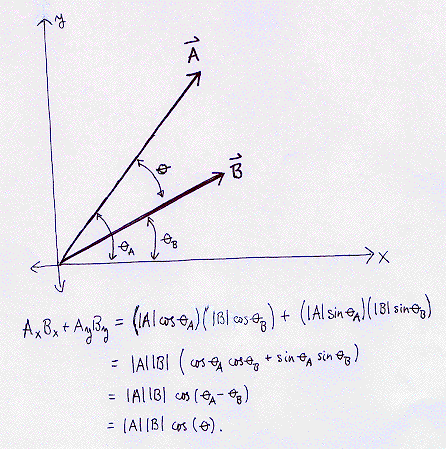
$A derivation of the cosine dot product definition via the component-wise dot product definition, from Dr. Seidler's website at the University of Washington from 1998$

Sources

The hand-drawn images for this page were taken from Dr. Seidler’s Winter 1998 Phys 121 page at the University of Washington (http://courses.washington.edu/phys121/stuquest/dot.html)